9.1.2. Operaciones criptográficas

Estudiaremos bajo este epígrafe las tres operaciones propias de la criptografía que nos permiten lograr los objetivos ya referidos:

• El resumen criptográfico, gracias a las funciones hash.

• El cifrado y cuáles son los algoritmos que se usan para ello.

• La firma digital, que es más bien un conjunto de operaciones que incluyen resumen y cifrado.

Nota

Tras la exposición teórica un apéndice práctico ilustra cómo llevar a cabo estas tareas en un sistema Linux, pero a efectos didácticos es más apropiado entremezclar teoría y práctica. La exposición no los entremezcla por si se desea usar herramientas distintas a las aquí propuestas.

9.1.2.1. Resumen criptográfico

Las funciones hash o funciones digest o funciones resumen son funciones que, dada una entrada, generan una salida, llamada resumen, caracterizada porque:

• siempre tiene el mismo tamaño, con independencia del tamaño de la entrada. Por tanto, si la función genera resúmenes de 256 bits, cualquier entrada se resumirá en 256 bits. La consecuencia de ello es que operan en un solo sentido, esto es, a partir del original obtenemos su resumen, pero a partir del resumen es imposible averiguar cuál era la información de partida.

• es determinista, esto es, para una misma entrada la salida siempre es la misma.

• se minimizan las colisiones, esto es, se minimiza la posibilidad de obtener una misma salida para dos entradas distintas.

La actividad de resumir criptográficamente la información está relacionada con el objetivo de la integridad, ya que dadas las propiedades de las funciones hash, es prácticamente imposible que un contenido que ha sufrido algún cambio, no cambie su resumen. En cualquier caso, aunque puede hacerse sin más el resumen de un archivo o un flujo de datos, lo habitual es que esta técnica criptográfica se integre dentro de la firma digital.

Entre las funciones de hash más conocidas se encuentran:

MD5

Genera un resumen de 128 bits representado habitualmente por 32 dígitos hexadecimales. Es muy común usarlo como comprobación de la integridad de ficheros. Su seguridad está en entredicho, ya que presenta problemas de colisiones.

SHA

Es una familia de funciones hash, diseñada originariamente por la NSA, que ha ido sufriendo diversas revisiones: SHA-0, SHA-1, SHA-2 y SHA-3. Tanto SHA-0 como SHA-1 generan resúmenes de 160 bits. Ambas se consideran inseguras y se desaconseja su uso. Para paliarlo, se desarrolló SHA-2, que implementa funciones hash de 224, 256, 364 y 512 bits. Se las conoce habitualmente como SHA-224, SHA-256, SHA-364 y SHA-512. SHA-3, por su parte, cambia internamente los algoritmos, pero está pensada para generar resúmenes de la misma longitud que SHA-2.

RIPEMD

Genera resúmenes de 128, 160, 256 y 320 bits y a diferencia del más popular SHA se desarrolló en la comunidad abierta. Su algoritmo original de 128 bits presenta colisiones, pero no las nuevas reformulaciones. RIPEMD-160 se usa dentro del cálculo de la dirección pública de un wallet de Bitcoin.

Ver también

Más adelante se ilustra cómo hacer resúmenes.

9.1.2.2. Cifrado

Por cifrado nos referimos particularmente a la acción de ofuscar cierta información con el objeto de que pueda ser posteriormente desofuscada. Si se ofusca con la intención de que sólo pueda deshacerla un tercero expresamente autorizado, entonces el cifrado tiene por objetivo la confidencialidad y tenemos propiamente aquello que comúnmente se refiere como cifrado. En cambio, si cualquier tercero puede desofuscar, el objetivo no es la privacidad, sino la autenticidad y entraríamos en el terreno de la firma digital, que trataremos más adelante.

Ya se ha comentado que los algoritmos modernos de cifrado se basan en el secreto de la clave y no en el secreto del propio algoritmo, por lo que nos centraremos en los algoritmos basados en clave. Atendiendo a ella hay dos tipos de algoritmos.

De clave simétrica

También conocidos como de clave privada o de clave única. Son aquellos en que se usa la misma clave para cifrar y descifrar.

De clave asimétrica

También conocidos como de clave pública o de doble clave. Son aquellos que emplean una pareja de claves, de manera que, si una se usó para cifrar un mensaje, la otra servirá para descifrarlo.

Son comunes las técnicas que usan combinadamente clave simétrica y asimétrica, lo cual se conoce como cifrado híbrido.

9.1.2.2.1. Cifrado simétrico

En este tipo de cifrado se usa la misma clave tanto para cifrar como para descifrar. El factor decisivo en la robustez de la clave es su longitud: cuanto más larga sea, más difícil es averiguarla por fuerza bruta. Por ejemplo, una clave de 8 bits sólo puede tener 2⁸, o sea, 256 valores distintos, lo que implica que podría adivinarse con un máximo de 256 intentos.

El punto débil de este cifrado es que, cuando el cifrado y el descifrado se llevan a cabo en puntos alejados, la clave debe encuentrarse en ambos extremos, lo cual se logra:

• Encontrándose previamente ambas partes para intercambiar en mano la clave, lo cual es costoso en tiempo y en recursos.

• Transmitiendo previamente la clave en claro, lo cual es sumamente arriesgado, porque puede provocar su intercepción y la inutilidad del cifrado posterior.

Algunos algoritmos de cifrado simétrico muy conocidos son:

DES

Considerado actualmente inseguro para la capacidad computacional de los ordenadores modernos, ya que tiene una longitud de sólo 56 bits. Su sucesor directo es el 3DES (Triple DES) que usa el triple de longitud para la clave (168 bits), aunque también se ha ido desplazando en favor de otros algoritmos.

AES

Sustituyó al algoritmo anterior y tiene una longitud de clave de 128, 192 ó 256 bits, aunque en teoría puede ser mayor[1]. Es más rápido y, además, no se le conocen vulnerabilidades. Es modernamente el algoritmo de clave simétrica más utilizado[2].

Existen otros algoritmos como Twofish, Serpent o Blowfish.

Ver también

Más adelante se ilustra cómo hacer cifrado simétrico con openssl.

9.1.2.2.2. Cifrado asimétrico

Se basa en el uso de una pareja de claves, una privada y otra pública generada a partir de ella, que se caracterizan por que lo que se haya cifrado con una sólo es posible descifrarlo con la otra. Por ello:

• La clave privada debe mantenerla en secreto su propietario.

• La clave pública se comunica a los demás.

De este modo, cuando se desease enviar un mensaje secreto a un destinatario, se podría usar la clave pública de éste, ya que tal mensaje sólo podría ser descifrado usando su clave privada correspondiente, que sólo está en posesión del destinatario. Por ello, el cifrado con la clave pública garantiza la privacidad.

Por otra parte, si un emisor usase su clave privada para cifrar, el mensaje podría descifrarse con su clave pública correspondiente. Como la clave pública es, eso mismo, pública, no sirve para salvaguardar ninguna privacidad, pero sí para asegurar que el emisor del mensaje es el dueño de las claves. Afinaremos esto más adelante[3].

Los algoritmos más conocidos de cifrado asimétrico son:

RSA

Es el primer sistema criptográfico de clave asimétrica y aún se considera válido (esto es, suficientemente seguro) tanto para cifrar y como firmar digitalmente. Por lo general, utiliza claves con una longitud entre 1024 y 4096 bits.

Los certificados digitales X.509 y PGP suelen incluir claves generadas con este algoritmo[4].

DSA

Es otro sistema criptográfico de clave asimétrica que en la actualidad se considera débil, por lo que se desaconseja su uso para cifrar información[5]. Sus claves tienen una longitud entre 512 y 1024 bits.

Variantes de este sistema que mejoran la fortaleza de las claves y, por tanto, permiten su uso para cifrado, son:

• ECDSA, que usa criptografía de curva elíptica.

• EdDSA, que usa también criptografía de curva elíptica. y se desarrolló para mejorar la velocidad de cifrado sin sacrificar seguridad. Un tipo particular de este sistema es Ed22519, que permiten usar las últimas versiones de openssh.

La desventaja fundamental del cifrado asimétrico frente al simétrico es su costo computacional: para un mismo nivel de seguridad requiere claves más largas y, además, para una misma longitud de clave es más costoso en tiempo. Este hecho determina que en la práctica el cifrado asimétrico sólo se utiliza para cifrar información muy breve.

Ver también

Más adelante se ilustra cómo hacer cifrado asimétrico con openssl.

9.1.2.2.3. Cifrado híbrido

De lo expuesto para los cífrados simétrico y asimétrico concluimos que:

• El cifrado asimétrico en la práctica habitual es inútil para cifrar información, por cuanto sólo es apto para cantidades muy pequeñas de información.

• El cifrado simétrico sí es válido, pero es intrínsecamente inseguro para transmitir información por cuanto nos obliga a enviar previamente (y, por tanto, en claro) la clave al otro extremo. Si el atacante ya escucha en este instante previo y captura la clave, todo el cifrado posterior, por bueno que sea el algoritmo con que se realiza, es inútil.

Estas conclusiones derivan en el problema de intercambio de clave, esto es, en resolver cómo intercambiar una clave simétrica de forma segura a través de un medio inseguro. Logrado esto, se dispondrá de una clave simétrica con la que cifrar la comunicación entre ambos extremos el tiempo que dure ésta (la llamada clave de sesión). Pero, en cualquier caso, es preciso resolver el problema de su seguridad. Hay dos alternativas habituales:

1. Intercambio de clave basado en clave pública

   Consiste en que uno de los extremos genera la clave simétrica, la cifra con la clave pública del otro extremo y se la envía cifrada. Al recibirla, este otro extremo la descifra con su clave privada y obtiene la clave simétrica que usarán ambos durante la comunicación.

2. Intercambio de clave Diffie-Hellman

   Consiste en que ambos extremos acuerdan en claro los parámetros que usarán (el módulo y la base) y generan ad hoc, cada uno por su cuenta, sendas claves privadas (\(x\) e \(y\)). Con estas claves y los parámetros, generan sendas claves públicas \(g^x\) y \(g^y\) que comunican a la otra parte. Las matemáticas involucradas propician que, cuando ambos aplican su propia clave privada sobre la clave pública recibida desde la otra parte (\((g^x)^y\) y \((g^y)^x\)), el resultado en ambas partes coincide y éste es la clave simétrica con la que cifrarán la comunicación (\(K = (g^x)^y = (g^y)^x\)). Un atacante que esté escuchando es capaz de capturar ambas claves públicas, pero no dispone de ninguna de las claves privadas, por lo que no podrá calcular la clave de sesión como hacen ambos extremos legítimos[6].

   Para ilustrar cómo funciona este mecanismo sin necesidad de entender las matemáticas subyacentes suele recurrirse a una analogía cromática:

   

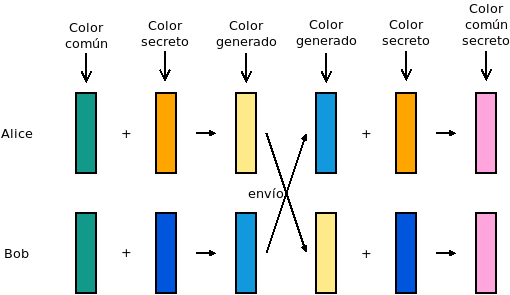
   O sea, Alice y Bob acuerdan un color base verdoso y cada uno de ellos por su cuenta escoge un color secreto (naranja y azul respectivamente). Componen un nuevo color con el color base y su color secreto y obtienen una mezcla (amarillo y azul claro, respectivamente) que sí publican comunicándolo al otro. Ambos finalmente mezclan el color comunicado con su propio color secreto y obtienen un mismo color resultante: una especie de violeta.

Las dos estrategias cumplen con el propósito y combinan una técnica inicial de cifrado asimétrico para establecer secretamente la clave de cifrado simétrico con la que se asegura finalmente la comunicación. Son, por tanto, técnicas de cifrado híbrido. Obsérvese, no obstante, que existe una diferencia capital entre ambas: la primera resolución utiliza una pareja de claves preexistente y persistente, mientras que la segunda usa un par de parejas de claves efímeras, que se crean para la ocasión y se abandonan acabada esta:

• La preexistencia determina que no haya que generar las claves asimétricas y, por tanto, se agilice el mecanismo para establecer el canal seguro.

• La persistencia de una pareja de claves permite que la otra parte pueda comprobar la identidad de su propietario. Por ejemplo, podemos estar seguros de que el otro extremo es quien dice ser, porque en una ocasión anterior nos entregó en mano su clave pública[7]. Esto con claves efímeras generadas ad hoc es imposible; lo que determina que un atacante pueda realizar un ataque MiTM.

• La efimeridad de las claves privadas mejora la seguridad, porque, si la la clave de sesión se cifró con la clave pública persistente de uno de los extremos, un atacante que haya guardado la conversación completa será incapaz de leerla en el momento; pero, si en el futuro logra hacerse con la clave privada, entonces podrá volver a recuperar la conversación y descrifrarla. Por contra, si las claves son efímeras, nunca se sufrirá este problema.

El cifrado híbrido es la base de todos los protocolos seguros de red como TLS/SSL o SSH. Para resolver el problema del intercambio de la clave simétrica estos protocolos pueden optar por una de las dos estrategias o dejar libertad para que alguno de los extremos escoja cuál prefiere. Sea cual sea la estrategia de intercambio, es indispensable que al menos el cliente se asegure de la identidad del servidor, por lo que para la identificación siempre se usa una técnica de clave pública.

Nota

Hemos centrado la explicación en la comunicación segura, pero el cifrado híbrido también es útil para cifrar previamente un archivo que queremos transmitir posteriormente mediante una comunicación no segura (p.e. el envío de un correo electrónico). En este caso, se usa la clave pública del destinatario para cifrar una clave simétrica con la que se ofusca la información y, ambas cosas, clave cifrada e informacion ofuscada, son las que se remiten.

9.1.2.2.4. Conclusiones

En vista de todo lo ya expuesto, lo adecuado al cifrar es usar:

1. Cifrado simétrico sobre:

   • Información que no se requiere transmitir (p.e. cifrado de disco).

   • Información que se transmite siempre que la clave simétrica se transmita cifrada asimétricamente, lo cual ya hemos definido como cifrado híbrido.

2. Cifrado asimétrico sobre una muy pequeña cantidad de información, esto es,

   • Sobre una clave simétrica que se desea transmitir, que es el complemento del cifrado híbrido que se acaba de citar.

   • Sobre un resumen criptográfico. Este acción de cifrado es propia de la firma digital; y la entenderemos a continuación.

9.1.2.3. Firma digital

En el mundo analógico, una firma manuscrita sobre papel es una marca que certifica que los términos expresados en un texto son ratificados por los firmantes. Por tanto, dejando al margen posibles falsificaciones, certifica la identidad de los participantes (autenticidad) y el contenido del texto (integridad).

Correspondientemente, una firma digital (o firma electrónica) es una técnica criptográfica que permite asegurar que unos datos (un archivo, un mensaje de correo, un flujo de datos) no han cambiado desde el momento en que los validaron uno o más suscribientes. Por ejemplo, el emisor de un correo electrónico puede firmar un mensaje para que el destinatario puede estar seguro de que él es el autor del mensaje y de que éste no ha sido alterado durante el proceso de comunicación.

La firma digital no es una operación atómica (criptográficamente hablando) como sí lo eran las dos anteriores de resumen y cifrado, sino un conjunto de dichas acciones que permite asegurar la identidad del emisor y la integridad del mensaje. Esquemáticamente, firmar es la operación resultante de:

1. Obtener un resumen de los datos mediante una función hash.

2. Cifrar tal resumen con la clave privada del firmante.

3. Añadir metainformacion relevante sobre la propia firma como cuándo se ha firmado o qué algoritmos se usaron para cifrar y resumir[8].

Hechas estas operaciones, podremos transmitir (o almacenar) los datos firmados como el conjunto de los datos originales, el resumen firmado y la metainformación relevante.

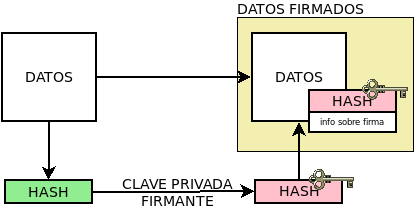
Ante esto, un tercero (por ejemplo, el destinatario de un mensaje de correo firmado), es capaz de certificar que el origen es quien dice ser, ya que descifrará el resumen con la clave pública de éste y, por otra parte, podrá comprobar si los datos conservan su integridad gracias al propio resumen descifrado[9].

Ver también

Más adelante se hace una primera aproximación a la firma digital intentando poner en práctica estos conceptos. Tenga presente, no obstante, que, en la realidad, son necesarios certificados digitales para asegurar la identidad real del firmante y, además, la firma se lleva a cabo mediante estándares que se expondrán al firmar documentos PDF o firmar mensajes de correo electrónico.

9.1.2.4. Apéndice práctico

Para poner en práctica los conceptos anteriores utilizaremos fundamentalmente OpenSSL. También podríamos usar GnuPG, que implementa el estándar OpenPGP; pero, dado que este estándar se usa fundamentalmente en el correo electrónico, introduciremos la orden en el epígrafe correspondiente.

Nota

En caso de que hagamos pruebas en una máquina virtual puede que sea conveniente aumentar la entropía del sistema para mejorar y acelerar la creación de claves asimétricas. Para lograrlo puede obrarse del siguiente modo[10]:

$ cat /proc/sys/kernel/random/entropy_avail  # Entropía inicial
234
# apt install rng-tools
# echo 'HRNGDEVICE=/dev/urandom' >> /etc/default/rng-tools
# echo 'RNGDOPTIONS="--fill-watermark=90%"' >> /etc/default/rng-tools
# invoke-rc.d rng-tools start
# cat /proc/sys/kernel/random/entropy_avail
2159

9.1.2.4.1. Resúmenes

Para la generación de resúmenes hash de ficheros y flujos de texto, existen dos órdenes fundamentales: md5sum y la familia de comandos shasum (sha256sum, sha384sum, sha512sum), que comparten una misma interfaz, con lo que es indiferente ilustrar el uso de una u otra orden. Suelen encontrarse todas instaladas en el sistema.

La generación del resumen puede hacerse del siguiente modo:

$ echo "Hola, caracola" > saludo1.txt
$ md5sum saludo1.txt
b18a245aba5384920d7f6a488d725181  saludo1.txt

Nota

Si se incluyen varios ficheros como argumento, se calculará el resumen de cada uno de ellos.

También es posible calcular el resumen de un flujo de datos:

$ echo "Hola, caracola" | sha256sum
d261be2aa264d38cad717fa8493dacc0b3f33f949869d39ecf7611689fb617ad  -

Habitualmente, los resúmenes generados se almacenan, a fin de que puedan servir más adelante para comprobar la integridad de los ficheros:

$ md5sum saludo1.txt saludo2.txt > saludos.md5

Con posterioridad, podrá comprobarse la integridad del siguiente modo[11]:

$ LC_ALL=C md5sum -c saludos.md5
saludo1.txt: OK
saludo2.txt: OK

Nota

Si se almacenó el resumen de un flujo de datos (obsérvese que aparece un «-», en vez de el nombre del fichero), puede comprobarse que otro flujo es el mismo pasándolo a través de la entrada estándar:

$ echo "Hola, caracola" | md5sum > flujo.md5
$ echo "Hola, caracola" | LC_ALL=C md5sum -c flujo.md5
-: OK

También es posible utilizar para este fin (aunque no es lo habitual) las herramientas que usaremos después para ilustrar el cifrado y la firma digital:

• GnuPG:

  $ gpg --print-md sha512 fichero.txt
  

  e incluso hay una opción que calcula los resúmenes según todos los algoritmos disponibles:

  $ gpg --print-mds fichero.txt
  

• OpenSSL:

  $ openssl dgst -sha512 fichero.txt
  

9.1.2.4.1.1. Cifrado simétrico

Una forma de llevarlo a cabo es esta:

$ openssl enc -aes256 -salt -pbkdf2 -a -in fichero.txt -out fichero.txt.enc

que utiliza AES-256 para el proceso y genera un cifrado en base64 gracias a la opción -a. Para descifrar basta con añadir la opción -d y, obviamente, utilizar como entrada el texto cifrado:

$ openssl enc -aes256 -pbkdf2 -a -d -in fichero.txt.enc -out fichero-recuperado.txt

Nota

Tanto -in como -out son opcionales y, si no se especifican, se entenderá que la entrada es la entrada estándar y la salida la salida estándar.

Nota

La clave simétrica para el cifrado/descifrado se pide de forma interactiva. Puede proporcionarse en la propia orden incluyendo la opción -pass:

$ openssl enc -aes256 -pbkdf2 -a -pass pass:clave-secreta -in fichero.txt -out fichero.txt.enc

Curiosidad

AES-256 requiere una clave de 256 bits para cifrar la información y nuestra contraseña, probablemente no tenga tal longitud. Por ese motivo, es necesario hacer un resumen criptográfico de la contraseña proporcionada. La orden propuesta fuerza a openssl con -salt a añadir una sal aleatoria a la contraseña y con -pdbkdf2 a aplicar iterativamente el algoritmo sha-256 un gran número de veces para obtener la clave de cifrado de 256 bits. Ambas opciones no son estrictamente necesarias, pero añaden mucha seguridad al resultado. Al descrifrar, -salt no es necesaria, porque debe guardarse junto a la información cifrada y, por consiguiente, openssl sabrá que tiene que añadirla a la contraseña que se proporcione cuando se pretende descifrar.

9.1.2.4.1.2. Cifrado asimétrico

Llevarlo a cabo requiere generar un par de claves (RSA en concreto[12]):

# openssl genrsa -aes128 -out privkey.pem 4096
# openssl rsa -in privkey.pem -pubout -out pubkey.pem

Las órdenes generan un par de claves RSA (privkey.pem y pubkey.pem) de 4096 bits. Para proteger la clave privada con una contraseña (esto es, con una clave simétrica) hemos usado la opción -aes128. Esto último es un simple mecanismo de seguridad para que sea imposible usar la clave privada sin conocer esta contraseña. Así, en caso de robo, el ladrón aún deberá averiguarla.

Nota

Las claves que se piden interactivamente pueden pasarse a través de las opciones -passin o -passout (vease openssl(1ssl) para más información)

Nota

Ambas claves usan para su información notación ASN.1 codificada en el formato binario DER que a continuación se recodifica en Base64 para que resulte un archivo imprimible. Lo mismo sucede con certificados digitales, archivos de firmas, etc. que iremos viendo a lo largo de este apéndice. Es por ello que todos los archivos tienen un aspecto semejante al consultarse con un cat:

$ cat pukey.pem
-----BEGIN PUBLIC KEY-----
MIIBIjANBgkqhkiG9w0BAQEFAAOCAQ8AMIIBCgKCAQEAxEUMJf+6dKU85GxWtbZv
gSwYqCMfydr7Pj0zNEd4QYEVnkqIny3qkreC5iBX1Afg1yl2XYDCI0IJW8iQ6e24
jS0FZkkHkbOjGMNwpyevdTNEItu0njgrl34HQ+fN89kauZQQUd32uaBW+QX4+zfl
pvRscvFNHkd90uLOzVymvx7n9xdNx+AScDdVpDz6Q/I9J2nB5YUSOemQiS3NpOLv
R7uEae0cPpEczuqX2kJzhxf+A/yteaJIR3fwZ4zcCNwsDRBhLSwXtYsYywdtNvf6
A1ZgmYPr7ZbqlWvd4BfROZNZlvm+OOVN1B51Z1GoSBGOTu/A6ZiRZGArveRUujtD
JwIDAQAB
-----END PUBLIC KEY-----

esto es, unas marcas de comienzo y final cuya leyenda exacta depende de qué se haya codificado (en el ejemplo, una clave pública) y una serie de caracteres imprimibles que son la citada Base64 del formato binario DER. En ocasiones openssl nos ofrece un modo de hacer legible la información almacenada y para el caso de claves RSA, lo hace:

$ openssl rsa -in privkey.pem -text -noout
$ openssl rsa -in pubkey.pem -pubin -text -noout

Obsérvese que ambas claves son pareja porque tienen el mismo módulo (que se puede consultar independientemente sustituyendo -text pòr -modulus)[13].

Con ellas podemos cifrar y descifrar pequeños[14] ficheros. Usando la clave pública para cifrar y la privada para descifrar:

# echo "Hola" > saludo.txt
# openssl rsautl -encrypt -inkey pubkey.pem -pubin -in saludo.txt -out saludo.enc
# openssl rsautl -decrypt -inkey privkey.pem -in saludo.enc
Hola

¿Podemos cifrar con la privada y descifrar con la pública? También:

# openssl rsautl -sign -inkey privkey.pem -in saludo.txt -out saludo.enc
# openssl rsautl -verify -inkey pubkey.pem -pubin -in saludo.enc
Hola

Nota

Si en vez de un un simple par de claves, tenemos un certificado digital, aún podremos realizar estas operaciones sustituyendo -pubin por -certin

9.1.2.4.1.3. Firma digital

Partiendo de las claves RSA ya generadas en el apartado anterior (privkey.pem, pubkey.pem), podemos hacer una primera aproximación tomando la descripción de lo que es la firma digital:

$ echo "Este es el contenido del fichero que firmo" > fichero.txt
$ sha256sum fichero.txt | tee /dev/tty | openssl rsautl -sign -inkey privkey.pem -out fichero.sign
47ebcc00b179c0f1fc8f45fec4a3e6a55fbb1aeddd8a5bb6ee52c5d7f57d1d3a  fichero.txt

Ya tenemos el archivo original (fichero.txt) y la firma (fichero.sign) generada con la clave privada. Con ellos dos y la clave publica correspondiente, podemos comprobar integridad e identidad:

$ sha256sum fichero.txt
47ebcc00b179c0f1fc8f45fec4a3e6a55fbb1aeddd8a5bb6ee52c5d7f57d1d3a  fichero.txt
$ openssl rsautl -verify -inkey pubkey.pem -pubin -in fichero.sign
47ebcc00b179c0f1fc8f45fec4a3e6a55fbb1aeddd8a5bb6ee52c5d7f57d1d3a  fichero.txt

Dado que coincide el resumen del archivo con la firma descifrada con la clave pública, podemos concluir que el archivo no ha cambiado y que lo certificó el propietario de la clave. En cualquier caso esto es sólo una aproximación al concepto ya que en una firma también es importante cuándo se produjo y con esta firma manual es imposible saberlo.

En realidad, para firmar con más comodidad, aunque nos abstraigamos del concepto:

$ openssl dgst -sha256 -sign privkey.pem -out fichero.sign fichero.txt

Y para verificar la firma:

$ openssl dgst -sha256 -verify pubkey.pem -signature fichero.sign fichero.txt
Verified OK

Nota

Cuando lo que se tiene no es un simple par de claves, sino un certificado digital aún puede hacerse este proceso extrayendo previamente la clave pública del certificado:

$ openssl x509 -in micert.pem -pubkey -nooout > pubkey.pem

aunque lo más adecuado, en realidad, sería firmar con S/MIME y OpenPGP[15].

Notas al pie

[1]

Para más información, puede leer esta respuesta de crypto.stackexchange.com.

[2]

AES fue el ganador de un concurso organizado en 1997 por la NIST para escoger un nuevo algoritmo de cifrado simétrico en sustitución de DES. De hecho, su nombre original es Rijndael, el nombre AES lo tomó de haberse constituido como el estándar.

[3]

Se ha usado en este párrafo y el anterior el condicional, porque teóricamente esto es así. En la práctica, el cifrado con clave asimétrica es muy costoso computacionalmente, así que se recurre a una argucia (el cifrado híbrido) pero reducir al máximo la cantidad de información que se cifra con clave asimétrica.

[4]

Pero no es obligatorio. Puedo probar a generar un certificado partiendo de una clave privada ECDSA generada con OpenSSL como se ilustra en el epígrafe en que se describe cómo convertir claves SSH en un formato inteligible por OpenSSL

[5]

De hecho, OpenSSH, para su versión 7, deshabilitó el uso de DSA (búsquese por DSS).

[6]

En realidad, llegar a calcularlo es tan extremadamente costoso computacionalmente que está fuera del alcance de cualquier supercomputador moderno.

[7]

¿Y si no es posible el contacto físico previo? Precisamente para eso existen los certificados digitales que introduciremos más adelante.

[8]

En puridad, hay parte de la metainformación que no nos interesa en absoluto que pueda ser adulterada (p.e. la fecha en la que se realiza la firma), por lo que habrá que incluirla dentro del resumen cifrado y no simplemente adjuntarla.

[9]

Pero para que todo esto no haga aguas es necesario confiar en que la clave pública es de aquel de quien parece ser. Resolveremos este último escollo al introducir el concepto de certificado digital.

[10]

Usar, sin embargo, el propio kernel para la generación de la entropía no es muy recomendable. Debería usarse el dispositivo hardware (/dev/hwrng), pero en la máquina virtual es posible que no esté. Para qemu véase su wiki.

[11]

Se fuerza a que la orden se ejecute en inglés, para que el resultado se exprese como OK o FAILED. En castellano, la leyenda se expresa de forma muy farragosa.

[12]

Podríamos también generar claves de curva elíptica. Hay algún ejemplo en el epígrafe en que se comparan las claves SSH con las generadas por OpenSSL.`

[13]

La clave pública se compone de un módulo y un exponente

[14]

Recordemos que el cifrado asimétrico está pensado para aplicarse sobre una cantidad muy pequeña de información (un resumen o una clave simétrica). La orden, de utilidad únicamente teórica, nos permite usar cifrado asimétrico puro sobre un archivo arbitrario, pero si este es grande generará un error (data too large for key size). Lo realista si queremos pasar a un tercero el archivo es utilizar cifrado híbrido (p.e. aplicando el estándar S/MIME con el proprio openssl).

[15]

Este procedimiento no es apropiado para firmar, porque en la realidad la validez de las claves no es eterna (como no lo es, por ejemplo, nuestro DNI). Todo esto se analizará al tratar los certificados digitales. Como no son eternas, cobra también importancia cuándo se firma, puesto que una firma válida sólo lo podrá ser dentro del periodo de tiempo en que las claves son válidas. En este procedimiento manual que hemos llevado a cabo no hay fechas (ni las claves tienen vigencia ni se sabe cuándo se ha llevado a cabo la firma). En consecuencia, no es un procedimiento adecuado para firmar con garantías.